01 Dec 2015
A substantial amount of scientific research is funded by investigator-initiated grants. A researcher has an idea, writes it up and sends a proposal to a funding agency. The agency then elicits help from a group of peers to evaluate competing proposals. Grants are awarded to the most highly ranked ideas. The percent awarded depends on how much funding gets allocated to these types of proposals. At the NIH, the largest funding agency of these types of grants, the success rate recently fell below 20% from a high above 35%. Part of the reason these percentages have fallen is to make room for large collaborative projects. Large projects seem to be increasing, and not just at the NIH. In Europe, for example, the Human Brain Project has an estimated cost of over 1 billion US$ over 10 years. To put this in perspective, 1 billion dollars can fund over 500 NIH R01s. R01 is the NIH mechanism most appropriate for investigator initiated proposals.
The merits of big science has been widely debated (for example here and here). And most agree that some big projects have been successful. However, in this post I present a statistical argument highlighting the importance of investigator-initiated awards. The idea is summarized in the graph below.
The two panes above represent two different funding strategies: fund-many-R01s (left) or reduce R01s to fund several large projects (right). The grey crosses represent investigators and the gold dots represent potential paradigm-shifting geniuses. Location on the Cartesian plane represent research areas, with the blue circles denoting areas that are prime for an important scientific advance. The largest scientific contributions occur when a gold dot falls in a blue circle. Large contributions also result from the accumulation of incremental work produced by grey crosses in the blue circles.
Although not perfect, the peer review approach implemented by most funding agencies appears to work quite well at weeding out unproductive researchers and unpromising ideas. They also seem to do well at spreading funds across general areas. For example NIH spreads funds across diseases and public health challenges (for example cancer, mental health, heart, genomics, heart and lung disease.) as well as general medicine, genomics and information. However, precisely predicting who will be a gold dot or what specific area will be a blue circle seems like an impossible endeavor. Increasing the number of tested ideas and researchers therefore increases our chance of success. When a funding agency decides to invest big in a specific area (green dollar signs) they are predicting the location of a blue circle. As funding flows into these areas, so do investigators (note the clusters). The total number of funded lead investigators also drops. The risk here is that if the dollar sign lands far from a blue dot, we pull researchers away from potentially fruitful areas. If after 10 years of funding, the Human Brain Project doesn’t “achieve a multi-level, integrated understanding of brain structure and function” we will have missed out on trying out 500 ideas by hundreds of different investigators. With a sample size this large, we expect at least a handful of these attempts to result in the type of impactful advance that justifies funding scientific research.
The simulation presented (code below) here is clearly an over simplification, but it does depict the statistical reason why I favor investigator-initiated grants. The simulation clearly depicts that the strategy of funding many investigator-initiated grants is key for the continued success of scientific research.
set.seed(2)
library(rafalib)
thecol=”gold3”
mypar(1,2,mar=c(0.5,0.5,2,0.5))
###
## Start with the many R01s model
###
##generate location of 2,000 investigators
N = 2000
x = runif(N)
y = runif(N)
## 1% are geniuses
Ng = N0.01
g = rep(4,N);g[1:Ng]=16
## generate location of important areas of research
M0 = 10
x0 = runif(M0)
y0 = runif(M0)
r0 = rep(0.03,M0)
##Make the plot
nullplot(xaxt=”n”,yaxt=”n”,main=”Many R01s”)
symbols(x0,y0,circles=r0,fg=”black”,bg=”blue”,
lwd=3,add=TRUE,inches=FALSE)
points(x,y,pch=g,col=ifelse(g==4,”grey”,thecol))
points(x,y,pch=g,col=ifelse(g==4,NA,thecol))
### Generate the location of 5 big projects
M1 = 5
x1 = runif(M1)
y1 = runif(M1)
##make initial plot
nullplot(xaxt=”n”,yaxt=”n”,main=”A Few Big Projects”)
symbols(x0,y0,circles=r0,fg=”black”,bg=”blue”,
lwd=3,add=TRUE,inches=FALSE)
### Generate location of investigators attracted
### to location of big projects. There are 1000 total
### investigators
Sigma = diag(2)0.005
N1 = 200
Ng1 = round(N10.01)
g1 = rep(4,N);g1[1:Ng1]=16
library(MASS)
for(i in 1:M1){
xy = mvrnorm(N1,c(x1[i],y1[i]),Sigma)
points(xy[,1],xy[,2],pch=g1,col=ifelse(g1==4,”grey”,thecol))
}
### generate location of investigators that ignore big projects
### note now 500 instead of 200. Note overall total
## is also less because large projects result in less
## lead investigators
N = 500
x = runif(N)
y = runif(N)
Ng = N0.01
g = rep(4,N);g[1:Ng]=16
points(x,y,pch=g,col=ifelse(g==4,”grey”,thecol))
points(x1,y1,pch=”$”,col=”darkgreen”,cex=2,lwd=2)
25 Nov 2015
Nick Carchedi is back visiting from DataCamp and for fun we came up with a [Nick Carchedi](http://nickcarchedi.com/) is back visiting from [DataCamp](https://www.datacamp.com/) and for fun we came up with a Rubik’s cube puzzle. Here is how it works. To solve the puzzle you have to make a 4 x 3 data frame that spells Thanksgiving like this:
To solve the puzzle you need to pipe this data frame in
and pipe out the Thanksgiving data frame using only the dplyr commands arrange, mutate, slice, filter and select. For advanced users you can try our slightly more complicated puzzle:
See if you can do it this fast. Post your solutions in the comments and Happy Thanksgiving!
24 Nov 2015
I finally got around to reading David Donoho’s 50 Years of Data Science paper. I highly recommend it. The following quote seems to summarize the sentiment that motivated the paper, as well as why it has resonated among academic statisticians:
The statistics profession is caught at a confusing moment: the activities which preoccupied it over centuries are now in the limelight, but those activities are claimed to be bright shiny new, and carried out by (although not actually invented by) upstarts and strangers.
The reason we started this blog over four years ago was because, as Jeff wrote in his inaugural post, we were “fired up about the new era where data is abundant and statisticians are scientists”. It was clear that many disciplines were becoming data-driven and that interest in data analysis was growing rapidly. We were further motivated because, despite this new found interest in our work, academic statisticians were, in general, more interested in the development of context free methods than in leveraging applied statistics to take leadership roles in data-driven projects. Meanwhile, great and highly visible applied statistics work was occurring in other fields such as astronomy, computational biology, computer science, political science and economics. So it was not completely surprising that some (bio)statistics departments were being left out from larger university-wide data science initiatives. Some of our posts exhorted academic departments to embrace larger numbers of applied statisticians:
[M]any of the giants of our discipline were very much interested in solving specific problems in genetics, agriculture, and the social sciences. In fact, many of today’s most widely-applied methods were originally inspired by insights gained by answering very specific scientific questions. I worry that the balance between application and theory has shifted too far away from applications. An unfortunate consequence is that our flagship journals, including our applied journals, are publishing too many methods seeking to solve many problems but actually solving none. By shifting some of our efforts to solving specific problems we will get closer to the essence of modern problems and will actually inspire more successful generalizable methods.
Donoho points out that John Tukey had a similar preoccupation 50 years ago:
For a long time I have thought I was a statistician, interested in inferences from the particular to the general. But as I have watched mathematical statistics evolve, I have had cause to wonder and to doubt. ... All in all I have come to feel that my central interest is in data analysis, which I take to include, among other things: procedures for analyzing data, techniques for interpreting the results of such procedures, ways of planning the gathering of data to make its analysis easier, more precise or more accurate, and all the machinery and results of (mathematical) statistics which apply to analyzing data
Many applied statisticians do the things Tukey mentions above. In the blog we have encouraged them to teach the gory details of what what they do, along with the general methodology we currently teach. With all this in mind, several months ago, when I was invited to give a talk at a department that was, at the time, deciphering their role in their university's data science initiative, I gave a talk titled 20 years of Data Science: from Music to Genomics. The goal was to explain why applied statistician is not considered synonymous with data scientist even when we focus on the same goal: extract knowledge or insights from data.
The first example in the talk related to how academic applied statisticians tend to emphasize the parts that will be most appreciated by our math stat colleagues and ignore the aspects that are today being heralded as the linchpins of data science. I used my thesis papers as examples. My dissertation work was about finding meaningful parametrization of musical sound signals that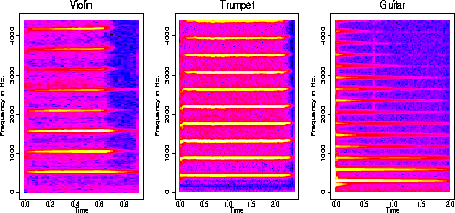
my collaborators could use to manipulate sounds to create new ones. To do this, I prepared a database of sounds, wrote code to extract and import the digital representations from CDs into S-plus (yes, I'm that old), visualized the data to motivate models, wrote code in C (or was it Fortran?) to make the analysis go faster, and tested these models with residual analysis by ear (you can listen to them here). None of these data science aspects were highlighted in the papers I wrote about my thesis. Here is a screen shot from this paper:
I am actually glad I wrote out and published all the technical details of this work. It was great training. My point was simply that based on the focus of these papers, this work would not be considered data science.
The rest of my talk described some of the work I did once I transitioned into applications in Biology. I was fortunate to have a department chair that appreciated lead-author papers in the subject matter journals as much as statistical methodology papers. This opened the door for me to become a full fledged applied statistician/data scientist. In the talk I described how developing software packages, planning the gathering of data to aid method development, developing web tools to assess data analysis techniques in the wild, and facilitating data-driven discovery in biology has been very gratifying and, simultaneously, helped my career. However, at some point, early in my career, senior members of my department encouraged me to write and submit a methods paper to a statistical journal to go along with every paper I sent to the subject matter journals. Although I do write methods papers when I think the ideas add to the statistical literature, I did not follow the advice to simply write papers for the sake of publishing in statistics journals. Note that if (bio)statistics departments require applied statisticians to do this, then it becomes harder to have an impact as data scientists. Departments that are not producing widely used methodology or successful and visible applied statistics projects (or both), should not be surprised when they are not included in data science initiatives. So, applied statistician, read that Tukey quote again, listen to President Obama, and go do some great data science.
19 Nov 2015
In response to my previous post, Avi Feller sent me these links related to efforts promoting the use of RCTs and evidence-based approaches for policymaking:
-
The theme of this year's just-concluded APPAM conference (the national public policy research organization) was "evidence-based policymaking," with a headline panel on using experiments in policy (see here and here).
-
Jeff Liebman has written extensively about the use of randomized experiments in policy (see here for a recent interview).
-
The White House now has an entire office devoted to running randomized trials to improve government performance (the so-called "nudge unit"). Check out their recent annual report here.
-
JPAL North America just launched a major initiative to help state and local governments run randomized trials (see here).
17 Nov 2015
Policy changes can have substantial societal effects. For example, clean water and hygiene policies have saved millions, if not billions, of lives. But effects are not always positive. For example, prohibition, or the “noble experiment”, boosted organized crime, slowed economic growth and increased deaths caused by tainted liquor. Good intentions do not guarantee desirable outcomes.
The medical establishment is well aware of the danger of basing decisions on the good intentions of doctors or biomedical researchers. For this reason, randomized controlled trials (RCTs) are the standard approach to determining if a new treatment is safe and effective. In these trials an objective assessment is achieved by assigning patients at random to a treatment or control group, and then comparing the outcomes in these two groups. Probability calculations are used to summarize the evidence in favor or against the new treatment. Modern RCTs are considered one of the greatest medical advances of the 20th century.
Despite their unprecedented success in medicine, RCTs have not been fully adopted outside of scientific fields. In this post, Ben Goldcare advocates for politicians to learn from scientists and base policy decisions on RCTs. He provides several examples in which results contradicted conventional wisdom. In this TED talk Esther Duflo convincingly argues that RCTs should be used to determine what interventions are best at fighting poverty. Although some RCTs are being conducted, they are still rare and oftentimes ignored by policymakers. For example, despite at least two RCTs finding that universal pre-K programs are not effective, polymakers in New York are implementing a $400 million a year program. Supporters of this noble endeavor defend their decision by pointing to observational studies and “expert” opinion that support their preconceived views. Before the 1950s, indifference to RCTs was common among medical doctors as well, and the outcomes were at times devastating.
Today, when we compare conclusions from non-RCT studies to RCTs, we note the unintended strong effects that preconceived notions can have. The first chapter in this book provides a summary and some examples. One example comes from a study of 51 studies on the effectiveness of the portacaval shunt. Here is table summarizing the conclusions of the 51 studies:
|
Design
|
Marked Improvement
|
Moderate Improvement
|
None
|
|
No control
|
24
|
7
|
1
|
|
Controls; but no randomized
|
10
|
3
|
2
|
|
Randomized
|
|
1
|
3
|
Compare the first and last column to appreciate the importance of the randomized trials.
A particularly troubling example relates to the studies on Diethylstilbestrol (DES). DES is a drug that was used to prevent spontaneous abortions. Five out of five studies using historical controls found the drug to be effective, yet all three randomized trials found the opposite. Before the randomized trials convinced doctors to stop using this drug , it was given to thousands of women. This turned out to be a tragedy as later studies showed DES has terrible side effects. Despite the doctors having the best intentions in mind, ignoring the randomized trials resulted in unintended consequences.
Well meaning experts are regularly implementing policies without really testing their effects. Although randomized trials are not always possible, it seems that they are rarely considered, in particular when the intentions are noble. Just like well-meaning turn-of-the-20th-century doctors, convinced that they were doing good, put their patients at risk by providing ineffective treatments, well intentioned policies may end up hurting society.
Update: A reader pointed me to these preprints which point out that the control group in one of the cited early education RCTs included children that receive care in a range of different settings, not just staying at home. This implies that the signal is attenuated if what we want to know is if the program is effective for children that would otherwise stay at home. In this preprint they use statistical methodology (principal stratification framework) to obtain separate estimates: the effect for children that would otherwise go to other center-based care and the effect for children that would otherwise stay at home. They find no effect for the former group but a significant effect for the latter. Note that in this analysis the effect being estimated is no longer based on groups assigned at random. Instead, model assumptions are used to infer the two effects. To avoid dependence on these assumptions we will have to perform an RCT with better defined controls. Also note that the RCT data facilitated the principal stratification framework analysis. I also want to restate what I’ve posted before, “I am not saying that observational studies are uninformative. If properly analyzed, observational data can be very valuable. For example, the data supporting smoking as a cause of lung cancer is all observational. Furthermore, there is an entire subfield within statistics (referred to as causal inference) that develops methodologies to deal with observational data. But unfortunately, observational data are commonly misinterpreted.”
Follow us on twitter 