Meet the Skeptics: Why Some Doubt Biomedical Models - and What it Takes to Win Them Over

Meet the Skeptics: Why Some Doubt Biomedical Models - and What it Takes to Win Them Over

Sunday data/statistics link roundup (7/1)

1. A really nice explanation of the elements of Obamacare. Rafa’s post on the new inHealth initiative Scott is leading got a lot of comments on Reddit. Some of them are funny (Rafa’s spelling got rocked) and if you get past the usual level of internet-commentary politeness, some of them seem to be really relevant - especially the comments about generalizability and the economics of health care. 
2. From Andrew J. a cool visualization of the human genome, they are showing every base of the human genome over the course of a year. That turns out to be about 100 bases per second. I think this is a great way to show how much information is in just one human genome. It also puts the sequencing data deluge in perspective. We are now sequencing thousands of these genomes a year and its only going to get faster. 
3. Cosma Shalizi has a nice list of unsolved problems in statistics on his blog (via Edo A.). These problems primarily fall into what I call Category 1 problems in my post on motivating statistical projects. I think he has some really nice insight though and some of these problems sound like a big deal if one was able to solve them.
4. A really provocative talk on why consumers are the job creators. The issue of who are the job creators seems absolutely ripe for a thorough statistical analysis. There are a thousand confounders here and my guess is that most of the work so far has been Category 2 - let’s use convenient data to make a stab at this. But a thorough and legitimate data analysis would be hugely impactful. 
5. Your eReader is collecting data about you.

Obamacare is not going to solve the health care crisis, but a new initiative, led by a statistician, may help

Obamacare may help protect a vulnerable section of our population, but it does nothing to solve the real problem with health care in the US: it is unsustainably expensive and getting worst worse. In the graph below (left) per capita medical expenditures for several countries are plotted against time. The US is the black curve, other countries are in grey. On the right we see life expectancy plotted against per capita medical expenditure. Note that the US spends $8,000 per person on healthcare, more than any other country and about 40% more than Norway, the runner up. If the US spent the same as Norway per person, as a country we would save ~ 1 trillion $ per year. Despite the massive investment, life expectancy in the US is comparable to Chile’s, a country that spends about $1,500 per person. To make matters worse, politicians and pundits greatly oversimply this problem by trying to blame their favorite villains while experts agree: no obvious solution exists.

This past Tuesday Johns Hopkins announced the launching of the Individualized Health Initiative. This effort will be led by Scott Zeger, a statistician and former chair of our department. The graphs and analysis shown above are from a presentation Scott has  shared on the web. The initiative’s goal is to “discover, test, and implement health information tools that allow the individual to understand, track, and guide his or her unique health state and its trajectory over time”. In other words, by tailoring treatments and prevention schemes for individuals we can improve their health more effectively.

1

49

284

Johns Hopkins University

2

1

332

14.0

96

800x600

So how is this going to help solve the health care crisis? Scott explains that when it comes to health care, Hopkins is a self-contained microcosm: we are the patients (all employees), the providers (hospital and health system), and the insurer (Hopkins is self-insured, we are not insured by for-profit companies). And just like the rest of the country, we spend way too much per person on health care. Now, because we are self-contained, it is much easier for us to try out and evaluate alternative strategies than it is for, say, a state or the federal government. Because we are large, we can gather enough data to learn about relatively small strata. And with a statistician in charge, we will evaluate strategies empirically as opposed to ideologically.  

Furthermore, because we are a University, we also employ Economists, Public Health Specialists, Ethicists, Basic Biologists, Engineers, Biomedical Researchers, and other scientists with expertise that seem indispensable to solve this problem. Under Scott’s leadership, I expect Hopkins to collect data more systematically, run well thought-out experiments to test novel ideas, leverage technology to improve diagnostics, and use existing data to create knowledge. Successful strategies may then be exported to the rest of the country. Part of the new institute’s mission is to incentivize our very creative community of academics to participate in this endeavor. 

Motivating statistical projects

It seems like half of the battle in statistics is identifying an important/unsolved problem. In math, this is easy, they have a list. So why is it harder for statistics? Since I have to think up projects to work on for my research group, for classes I teach, and for exams we give, I have spent some time thinking about ways that research problems in statistics arise.

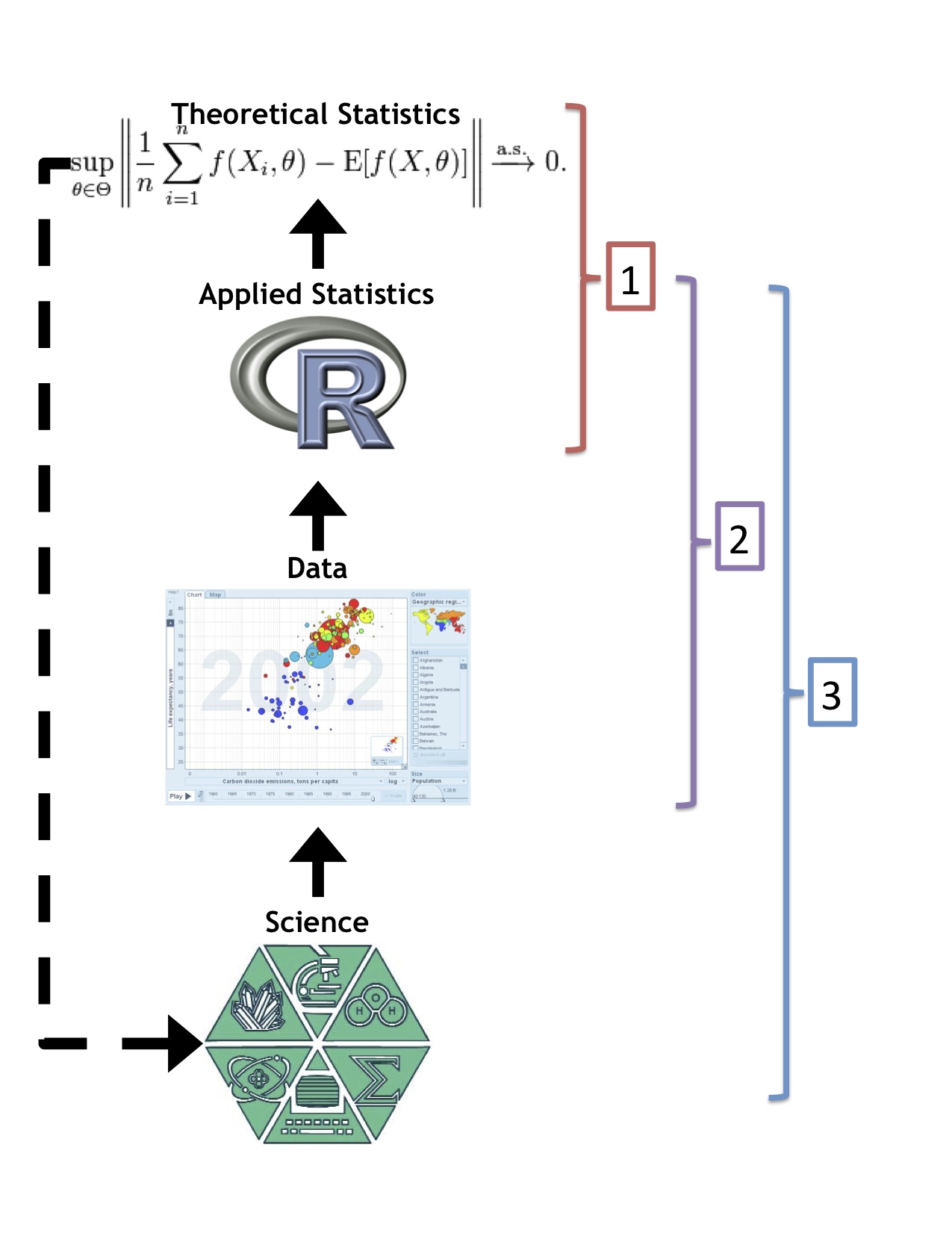
I borrowed a page out of Roger’s book and made a little diagram to illustrate my ideas (actually I can’t even claim credit, it was Roger’s idea to make the diagram). The diagram shows the rough relationship of science, data, applied statistics, and theoretical statistics. Science produces data (although there are other sources), the data are analyzed using applied statistical methods, and theoretical statistics concerns the math behind statistical methods. The dotted line indicates that theoretical statistics ostensibly generalizes applied statistical methods so they can be applied in other disciplines. I do think that this type of generalization is becoming harder and harder as theoretical statistics becomes farther and farther removed from the underlying science.

Based on this diagram I see three major sources for statistical problems: 

1. Theoretical statistical problems One component of statistics is developing the mathematical and foundational theory that proves we are doing sensible things. This type of problem often seems to be inspired by popular methods that exists/are developed but lack mathematical detail. Not surprisingly, much of the work in this area is motivated by what is mathematically possible or convenient, rather than by concrete questions that are of concern to the scientific community. This work is important, but the current distance between theoretical statistics and science suggests that the impact will be limited primarily to the theoretical statistics community. 
2. Applied statistics motivated by convenient sources of data. The best example of this type of problem are the analyses in Freakonomics.  Since both big data and small big data are now abundant, anyone with a laptop and an internet connection can download the Google n-gram data, a microarray from GEO , data about your city, or really data about anything and perform an applied analysis. These analyses may not be straightforward for computational/statistical reasons and may even require the development of new methods. These problems are often very interesting/clever and so are often the types of analyses you hear about in newspaper articles about “Big Data”. But they may often be misleading or incorrect, since the underlying questions are not necessarily well founded in scientific questions. 
3. Applied statistics problems motivated by scientific problems. The final category of statistics problems are those that are motivated by concrete scientific questions. The new sources of big data don’t necessarily make these problems any easier. They still start with a specific question for which the data may not be convenient and the math is often intractable. But the potential impact of solving a concrete scientific problem is huge, especially if many people who are generating data have a similar problem. Some examples of problems like this are: can we tell if one batch of beer is better than another, how are quantitative characteristics inherited from parent to child, which treatment is better when some people are censored, how do we estimate variance when we don’t know the distribution of the data, or how do we know which variable is important when we have millions? 

So this leads back to the question, what are the biggest open problems in statistics? I would define these problems as the “high potential impact” problems from category 3. To answer this question, I think we need to ask ourselves, what are the most common problems people are trying to solve with data but can’t with what is available right now? Roger nailed this when he talked about the role of statisticians in the science club. 

Here are a few ideas that could potentially turn into high-impact statistical problems, maybe our readers can think of better ones?

1. How do we credential students taking online courses at a huge scale?
2. How do we communicate risk about personalized medicine (or anything else) to a general population without statistical training? 
3. Can you use social media as a preventative health tool?
4. Can we perform randomized trials to improve public policy?

The price of skepticism

Thanks to John Cook for posting this:

“If you’re only skeptical, then no new ideas make it through to you. You never can learn anything. You become a crotchety misanthrope convinced that nonsense is ruling the world.” – Carl Sagan